Поиск в глубину на ориентированном графе

Поиск в глубину на ориентированном графе. Алгоритм построения ациклического орграфа

1. Постановка задачи

На практике часто возникает задача о размыкании всех контуров (ориентированных циклов) орграфа путём удаления минимального числа дуг (ориентированных рёбер).

Например, в системе Oracle производственные задания вида (Позиция_1|Склад_1)(Позиция_2|Склад_2), участвующие в расчете себестоимости продукции, образуют множество E дуг орграфа G = <V, E>. Множество вершин V состоит из пар вида (Позиция|Склад). Если построенный таким образом граф G содержит контуры (бракованная продукция стала снова исходным сырьём), то процедура расчёта себестоимости зацикливается.

Таким образом, перед запуском процедуры расчёта себестоимости необходимо разомкнуть все контуры и превратить орграф в ациклический. Для неориентированного графа эта задача решается поиском в глубину (ПВГ). С помощью ПВГ необходимо определить множество m – n + p хорд (m – количество рёбер, n – количество вершин, p – количество компонент связности неориентированного графа), замыкающих фундаментальные циклы графа, а затем удалить их из графа.
В ориентированном графе не существует множества фундаментальных ориентированных циклов, так как множество ориентированных циклов не образует линейного пространства (результат операции сложения двух ориентированных циклов по mod 2 не является ориентированным циклом). Тем не менее, орграф можно превратить в ациклический с помощью линейного алгоритма [1].

Для этого нужно рассмотреть ПВГ для ориентированного графа. Для машинного представления орграфа будем использовать списки инцидентности. Cписки инцидентности орграфа бывают двух типов: списки предыдущих вершин и списки следующих вершин. Для работы нам понадобятся только списки следующих вершин, которые обозначим L.

2. Поиск в глубину на ориентированном графе

Каждая вершина орграфа может находиться в одном из трех состояний: новая, просмотренная, использованная (вытолкнутая из стека). Для дальнейшего использования будем присваивать каждой просмотренной вершине v номер GLN[v] – порядок просмотра при поиске в глубину. Переход от старой вершины к новой будет происходить по спискам инцидентности L, согласованным с ориентацией дуг.

АЛГОРИТМ {Поиск в глубину на ориентированном графе}
Данные: орграф G = <V,E >, представленный списками инцидентности следующих вершин L[v], v ε V, |V| = n.

Результаты: обход всех вершин орграфа поиском в глубину.

Глобальные переменные: GLN, num.

Procedure GL(v: вершина); {поиск в глубину из вершины v}
1 begin
2     num:= num+1; {увеличиваем текущий номер}
3     GLN[v]:= num;  {нумеруем текущую вершину}
4     for u Î L[v] do {перебор вершин, инцидентных v согласно ориентации дуг}
5         if GLN[u] = 0 then {нашли новую вершину}
6           GL(u); {продолжаем поиск из вершины u)
7 end;
1 begin {основная программа}
2     for v:=1 to n do GLN[v]:= 0; {все вершины новые}
3     num:=0;
4     for v:=1 to n do
5        if GLN[v] = 0 then GL(v);
7 end.

Процедура ПВГ на ориентированном графе строит ориентированный остовный лес, то есть множество вершин графа V разбивается на непересекающиеся множества V1, V2, … Vk, причем каждое Vi является множеством вершин ориентированного корневого дерева T_i. Заметим, что каждая вершина орграфа содержится в том или ином корневом дереве, но некоторые дуги орграфа могут не входить ни в одно корневое дерево.

3. Разбиение дуг орграфа при поиске в глубину

В процессе обхода неориентированного графа поиском в глубину множество дуг разбивается на два непересекающихся множества – ветви и хорды.

В процессе обхода орграфа поиском в глубину все множество дуг разбивается на четыре непересекающиеся множества и только одно из них – множество обратных дуг – является множеством дуг, замыкающих ориентированные циклы.

Первое множество – это множество ветвей ориентированного корневого дерева, соединяющих отца v с его сыном u по поиску в глубину (строки 4–5 процедуры GL). Такие дуги называются ветвями корневого дерева, вершина v называется отец, вершина u – сын.

Возможен случай, когда в цикле строки 4 процедуры GL для вершины v мы находим просмотренную вершину u, причем GLN[v]<GLN[u]. Это означает, что для вершины v мы нашли ее потомка относительно поиска в глубину. Такие дуги образуют второе множество прямых дуг, вершина v называется предок, вершина u – потомок.

Кроме того, две просмотренные вершины u и v могут не быть ни предками, ни потомками друг друга. Например, вершина v может иметь двух сыновей, соединенных между собой дугой от младшего сына (с большим номером) к старшему сыну (с меньшим номером). Другой пример – это дуги, которые не входят ни в одно корневое дерево. Такие дуги образуют третье множество поперечных дуг. Их можно определить по следующему правилу. Если в строке 4 для вершины v мы находим вершину u, которая уже использована (вытолкнута из стека), то дугаv→u – поперечная.

Наконец, если дуга v→u идет от потомка к предку, то эта дуга замыкает ориентированный цикл. Такие дуги образуют четвёртое множество обратных дуг.
Условие обратной дуги: обе вершины u и v просмотрены, обе находятся в стеке и GLN[v] >GLN[u].

Понятно, что если при обходе графа ПВГ встретилась обратная дуга, то найден ориентированный цикл. Докажем обратное утверждение.

Утверждение 1. Если в орграфе есть контур (ориентированный цикл), то замыкающая его обратная дуга обязательно встретится при поиске в глубину.

Доказательство. Предположим, что орграф G имеет контур. Так как поиск в глубину просматривает все вершины графа, то все вершины, входящие в контур, получат номера GLN. Выберем вершину v, имеющую наименьший номер GLN[v]. Рассмотрим дугу v→u принадлежащую этому циклу. Поскольку от v до u можно дойти по дугам цикла и v имеет меньший номер, чем u, u является потомком v в ориентированном корневом дереве, следовательно, дуга не может быть поперечной. Так как GLN[v] < GLN[u], то дуга v→u не может быть прямой дугой v→u или ветвью каркаса. Следовательно, дуга v→u обратная и будет найдена при построении корневого дерева, содержащего вершину v.

Очевидным следствием из утверждения 1 является утверждение 2.

Утверждение 2. Удаление из орграфа всех обратных дуг, найденных при поиске в глубину, превратит орграф в ациклический.

Таким образом, относительно своего корневого дерева T_iкаждая обратная дугазамыкает ровно один ориентированный цикл, и все эти циклы различны, а в исходном графе G каждая обратная дуга может замыкать несколько различных циклов.

4. Алгоритм нахождения множества обратных дуг

АЛГОРИТМ {Нахождение множества обратных дуг}

Данные: орграф G = <V,E >, представленный списками инцидентности L[v], v ε V, |V| = n.

Результаты: печать обратных дуг и контуров, которые они замыкают.

Глобальные переменные: GLN, STACK, InStack, num, d.

Procedure CYCLE(v: вершина);
1  begin
2      num:= num+1; {увеличиваем текущий номер}
3      GLN[v]:= num; {нумеруем  вершину v}
4      d:= d+1; {увеличиваем длину стека}
5      STACK[d]:= v; {помещаем вершину в стек}
6      InStack[v]:= true;
7      for u Î L[v] do {перебор вершин, инцидентных v согласно ориентации дуг} 
8          if GLN[u] = 0 then //нашли ветвь дерева
9            GL(u) {продолжили поиск из вершины u}
10        if else (GLN[v]>GLN[u]) AND InStack[u] then  {нашли обратную дугу}
11           печать дуги и цикла от верхушки стека до вершины u;
12    d:= d-1; {вершина v использована и удаляется из стека} 
13    InStack[v]:=false;
14 end;

1 begin  {основная программа}
2     for v:=1 to n do GLN[v]:= 0; {все вершины новые}
3     for v:=1 to n do InStack[v]:= 0; {все вершины не в стеке}
4     num:=0; {текущий номер}
5     d:=0; {текущая длина стека}
6     for v:=1 to n do
7         if GLN[v] = 0 then CYCLE(v); {запускаем поиск из каждой новой вершины}
8 end.

Вычислительная сложность процедуры CYCLE O(nm) или O(n³), где n – количество вершин графа.

5. Трассировка алгоритма нахождения обратных дуг

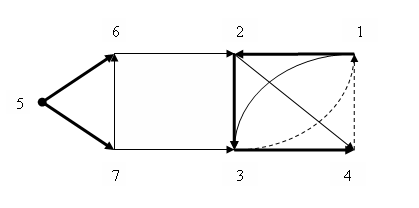
Рассмотрим модельный граф G, изображенный на рисунке. Жирными линиями изображены корневые деревья, сплошными линиями обычной толщины – прямые и поперечные дуги, штриховыми линиями – обратные дуги.